
Introduction to magrene
Fabricio Almeida-Silva
VIB-UGent Center for Plant Systems Biology, Ghent, BelgiumDepartment of Plant Biotechnology and Bioinformatics, Ghent University, Ghent, BelgiumYves Van de Peer
VIB-UGent Center for Plant Systems Biology, Ghent, BelgiumDepartment of Plant Biotechnology and Bioinformatics, Ghent University, Ghent, BelgiumCollege of Horticulture, Academy for Advanced Interdisciplinary Studies, Nanjing Agricultural University, Nanjing, ChinaCenter for Microbial Ecology and Genomics, Department of Biochemistry, Genetics and Microbiology, University of Pretoria, Pretoria, South Africa2023-03-14
Source:vignettes/magrene.Rmd
magrene.RmdIntroduction
Network motifs are the building blocks of complex networks, and they
can be interpreted as small genetic circuits. Identifying and counting
motifs in gene regulatory networks can reveal important aspects of the
evolution of transcriptional regulation. In particular, they can be used
to explore the impact of gene duplication in the rewiring of regulatory
interactions (Mottes et al. 2021).
magrene aims to identify and analyze motifs in (duplicated)
gene regulatory networks to better comprehend the role of gene
duplication in network evolution. The figure below shows the networks
motifs users can identify with magrene.
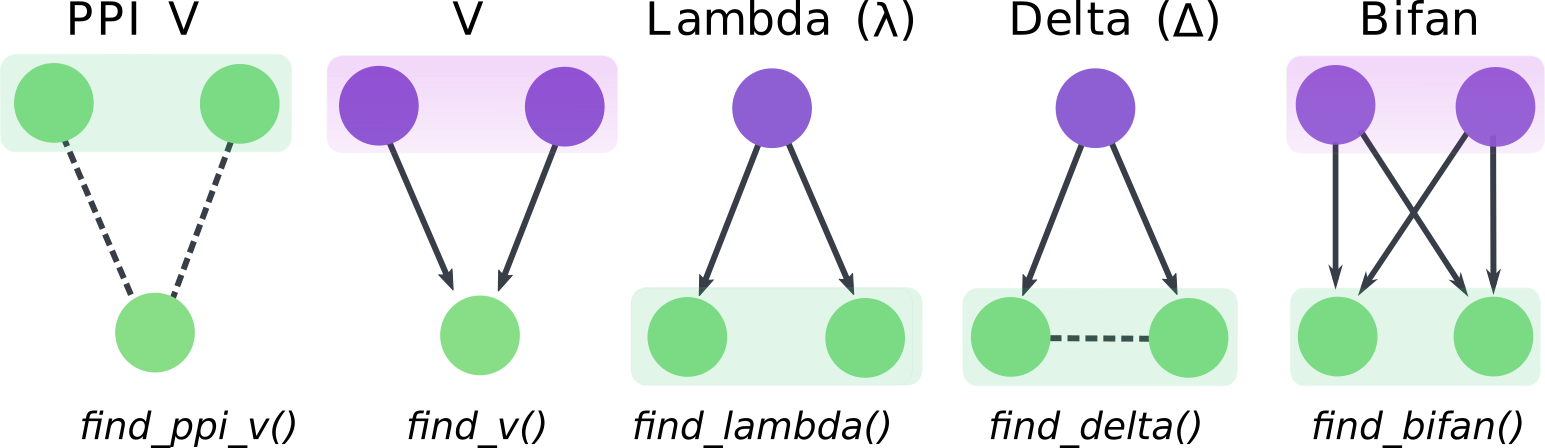
Network motifs and functions to identify them. Shaded boxes indicate paralogs. Regulators and targets are indicated in purple and green, respectively. Arrows indicate directed regulatory interactions, while dashed lines indicate protein-protein interaction.
Installation
You can install magrene with:
if (!requireNamespace("BiocManager", quietly = TRUE)) {
install.packages("BiocManager")
}
BiocManager::install("magrene")Then, you can load the package with:
Data description
For this vignette, we will use three example data sets:
gma_grn: A gene regulatory network inferred with
BioNERO(Almeida-Silva and Venancio 2022) using soybean RNA-seq data from the Soybean Expression Atlas (Machado et al. 2020).gma_ppi: A protein-protein interaction (PPI) network for soybean obtained from the STRING database (Szklarczyk et al. 2021), filtered to contain only physical interactions with confidence score > 0.4.
gma_paralogs: Soybean paralogous gene pairs derived by whole-genome, tandem, proximal, transposed, and dispersed duplications (WGD, TD, PD, TRD, and DD, respectively). This data set was obtained from Almeida-Silva et al. (2020).
Networks are represented as edge lists. Let’s take a look at the data.
data(gma_grn)
head(gma_grn)
#> Node1 Node2 Weight
#> 615572 Glyma.20G042000 Glyma.13G027300 0.09219597
#> 177435 Glyma.06G225200 Glyma.04G205700 0.09054177
#> 208602 Glyma.09G278100 Glyma.05G084800 0.08846030
#> 190115 Glyma.18G039200 Glyma.05G002100 0.08382400
#> 78998 Glyma.01G075800 Glyma.02G221200 0.08271081
#> 870271 Glyma.09G231700 Glyma.18G220700 0.08208945
data(gma_ppi)
head(gma_ppi)
#> node1 node2
#> 4971 Glyma.19G213200 Glyma.01G004300
#> 4985 Glyma.14G061100 Glyma.01G004300
#> 4995 Glyma.03G179000 Glyma.01G004300
#> 5021 Glyma.03G097900 Glyma.01G004300
#> 5037 Glyma.07G047700 Glyma.01G004300
#> 5053 Glyma.19G051900 Glyma.01G004300
data(gma_paralogs)
head(gma_paralogs)
#> duplicate1 duplicate2 type
#> 1 Glyma.01G007200 Glyma.01G007300 TD
#> 2 Glyma.01G007400 Glyma.01G007500 TD
#> 3 Glyma.01G011500 Glyma.01G011600 TD
#> 4 Glyma.01G012100 Glyma.01G012200 TD
#> 5 Glyma.01G015200 Glyma.01G015300 TD
#> 6 Glyma.01G020600 Glyma.01G020700 TDFinding motifs
Motifs can be found using find_* motifs, as shown in
Figure 1. Each function returns a character vector of motifs, and each
motif has its own character representation. Let’s demonstrate how they
work. For the sake of demonstration, we will only use WGD-derived
paralogs. For GRN motifs, we will only use a smaller subset of the edge
list.
# Include only WGD-derived paralogs
paralogs <- gma_paralogs[gma_paralogs$type == "WGD", 1:2]
# Keep only the top 30k edges of the GRN, remove "Weight" variable
grn <- gma_grn[1:30000, 1:2]PPI V
PPI V motifs are paralogous proteins that share an interaction
partner. To find them, you will use find_ppi_v(). The
character representation of PPI V motifs is:
\[ \text{paralog1-partner-paralog2} \]
# Find PPI V motifs
ppi_v <- find_ppi_v(gma_ppi, paralogs)
head(ppi_v)
#> [1] "Glyma.19G213200-Glyma.01G004300-Glyma.03G216600"
#> [2] "Glyma.07G034300-Glyma.01G004300-Glyma.08G207800"
#> [3] "Glyma.14G101700-Glyma.01G004300-Glyma.06G061100"
#> [4] "Glyma.12G028500-Glyma.01G004300-Glyma.11G103700"
#> [5] "Glyma.19G189600-Glyma.01G004300-Glyma.03G189300"
#> [6] "Glyma.15G006700-Glyma.01G004300-Glyma.07G029200"V
V motifs are paralogous regulators that regulate the same target.
These motifs can be created when a regulator undergoes a small-scale
duplication. To find them, you will use find_v(). The
character representation of V motifs is:
\[ \text{regulator->target<-regulator} \]
# Find V motifs
v <- find_v(grn, paralogs)
head(v)
#> [1] "Glyma.01G177200<-Glyma.16G128800->Glyma.02G058700"
#> [2] "Glyma.01G177200<-Glyma.08G362400->Glyma.02G058700"
#> [3] "Glyma.01G177200<-Glyma.02G103700->Glyma.02G058700"
#> [4] "Glyma.01G177200<-Glyma.09G152400->Glyma.02G058700"
#> [5] "Glyma.01G177200<-Glyma.20G151800->Glyma.02G058700"
#> [6] "Glyma.01G177200<-Glyma.08G020300->Glyma.02G058700"Lambda
Lambda motifs are the opposite of V motifs: a single regulator that
regulates two target genes that are paralogous. These motifs can be
created when an ancestral target gene undergoes a small-scale
duplication. To find them you will use find_lambda(). The
character representation of lambda motifs is:
\[ \text{target1<-regulator->target2} \]
lambda <- find_lambda(grn, paralogs)
head(lambda)
#> [1] "Glyma.01G132800<-Glyma.07G126500->Glyma.03G035400"
#> [2] "Glyma.01G205300<-Glyma.07G126500->Glyma.05G064600"
#> [3] "Glyma.01G205300<-Glyma.08G227000->Glyma.05G064600"
#> [4] "Glyma.01G205300<-Glyma.07G128700->Glyma.05G064600"
#> [5] "Glyma.01G205300<-Glyma.07G087900->Glyma.05G064600"
#> [6] "Glyma.01G205300<-Glyma.19G022200->Glyma.05G064600"Delta
Delta motifs are pretty similar to lambda motifs, but here we take
protein-protein interactions between targets into account. Thus, they
are represented by a regulator that regulates two targets that interact
at the protein level. They can be created by the same evolutionary
mechanism of lambda motifs. To find them, you will use
find_delta(). The character representation of delta motifs
is:
\[ \text{target1<-regulator->target2} \]
To find delta motifs, you have two options:
Pass PPI edge list + a vector of previously identified lambda motifs (recommended).
Pass PPI edge list + GRN edge list + paralogs data frame. In this option,
find_delta()will find lambda motifs first, then use the lambda vector to find delta motifs. If you have identified lambda motifs beforehand, it is way faster to pass the lambda vector tofind_delta(), so you don’t have to do double work.
# Find delta motifs from lambda motifs
delta <- find_delta(edgelist_ppi = gma_ppi, lambda_vec = lambda)
head(delta)
#> [1] "Glyma.10G242600<-Glyma.04G221800->Glyma.20G151500"Bifan
Bifan motifs are the most complex: they are represented by two
paralogous regulators that regulate the same set of two paralogous
targets. They can be created when both the ancestral regulator and the
ancestral target are duplicated by small-scale duplications, or when the
genome undergoes a whole-genome duplication event. To find these motifs,
you will use find_bifan(). The character representation of
bifan motifs is:
\[ \text{regulator1,regulator2->target1,target2} \]
Under the hood, what find_bifan() does it to find lambda
motifs involving the same targets and check if their regulators are
paralogs. Thus, if you have identified lambda motifs beforehand, it is
much faster to simply give them to find_bifan(), so it
doesn’t have to find them again.
# Find bifans from lambda motifs
bifan <- find_bifan(paralogs = paralogs, lambda_vec = lambda)
head(bifan)
#> [1] "Glyma.01G177200,Glyma.02G058700->Glyma.09G152400,Glyma.20G151800"Counting motifs and evaluating significance
As motifs are simple character vectors, one can count their
frequencies with the base R length() function. For example,
let’s count the frequency of each motif in our example data set:
count_df <- data.frame(
Motif = c("PPI V", "V", "Lambda", "Delta", "Bifan"),
Count = c(
length(ppi_v), length(v), length(lambda), length(delta), length(bifan)
)
)
count_df
#> Motif Count
#> 1 PPI V 1521
#> 2 V 112
#> 3 Lambda 163
#> 4 Delta 1
#> 5 Bifan 1However, unless you have another data set to which you can compare
your frequencies, counting is not enough. You need to evaluate the
significance of your motif frequencies. One way to do that is by
comparing your observed frequencies to a null distribution generated by
counting motifs in N (e.g., 1000) simulated networks 1.
magrene allows you to generate null distributions of motif
frequencies for each motif type with the function
generate_nulls(). As generating the null distributions
takes a bit of time, we will demonstrate generate_nulls()
with 5 permutations only. As a rule of thumb, you would probably want
N >= 1000.
generate_nulls(grn, paralogs, gma_ppi, n = 5)
#> $lambda
#> lambda lambda lambda lambda lambda
#> 79 81 92 87 83
#>
#> $delta
#> delta delta delta delta delta
#> 7 2 6 5 7
#>
#> $V
#> V V V V V
#> 121 138 126 122 139
#>
#> $PPI_V
#> PPI_V PPI_V PPI_V PPI_V PPI_V
#> 189 195 178 163 168
#>
#> $bifan
#> bifan bifan bifan bifan bifan
#> 0 0 0 0 0As you can see, the output of generate_nulls() is a list
of numeric vectors with the frequency of each motif type in the
simulated networks2. You can use the null distribution to
calculate Z-scores for your observed frequencies, which are defined as
below:
\[ Z = \frac{ n_{observed} - \bar{n}_{null} }{ \sigma_{null} } \]
To calculate Z-scores, you can use the function
calculate_Z(). As input, you need to give a list of
observed frequencies and a list of nulls. Here, we will load
pre-computed null distributions of N = 100.
# Load null distros
data(nulls)
head(nulls)
#> $lambda
#> lambda lambda lambda lambda lambda lambda lambda lambda lambda lambda lambda
#> 76 84 80 88 77 83 81 85 83 79 89
#> lambda lambda lambda lambda lambda lambda lambda lambda lambda lambda lambda
#> 77 87 78 88 82 87 70 89 82 78 78
#> lambda lambda lambda lambda lambda lambda lambda lambda lambda lambda lambda
#> 93 75 69 92 86 95 78 90 86 95 94
#> lambda lambda lambda lambda lambda lambda lambda lambda lambda lambda lambda
#> 80 100 93 92 100 79 71 83 92 74 78
#> lambda lambda lambda lambda lambda lambda lambda lambda lambda lambda lambda
#> 103 89 91 84 85 89 78 81 71 89 83
#> lambda lambda lambda lambda lambda lambda lambda lambda lambda lambda lambda
#> 103 84 101 93 98 77 95 88 78 98 86
#> lambda lambda lambda lambda lambda lambda lambda lambda lambda lambda lambda
#> 70 82 82 78 75 86 100 83 96 78 93
#> lambda lambda lambda lambda lambda lambda lambda lambda lambda lambda lambda
#> 94 82 65 85 83 83 74 100 87 78 78
#> lambda lambda lambda lambda lambda lambda lambda lambda lambda lambda lambda
#> 94 84 97 82 90 113 81 76 96 88 87
#> lambda
#> 91
#>
#> $delta
#> delta delta delta delta delta delta delta delta delta delta delta delta delta
#> 1 4 2 8 6 5 3 0 1 7 2 1 3
#> delta delta delta delta delta delta delta delta delta delta delta delta delta
#> 1 2 1 2 1 2 3 7 1 4 4 3 1
#> delta delta delta delta delta delta delta delta delta delta delta delta delta
#> 3 3 3 4 3 2 1 2 2 6 7 4 1
#> delta delta delta delta delta delta delta delta delta delta delta delta delta
#> 2 5 1 1 0 1 2 6 6 6 9 2 2
#> delta delta delta delta delta delta delta delta delta delta delta delta delta
#> 3 4 3 3 4 4 4 3 2 1 2 8 7
#> delta delta delta delta delta delta delta delta delta delta delta delta delta
#> 4 4 4 1 3 2 7 4 2 2 4 5 6
#> delta delta delta delta delta delta delta delta delta delta delta delta delta
#> 3 2 3 2 4 3 3 1 2 1 2 2 7
#> delta delta delta delta delta delta delta delta delta
#> 0 4 4 3 1 1 5 3 2
#>
#> $V
#> V V V V V V V V V V V V V V V V V V V V
#> 133 131 136 130 123 112 126 117 124 130 128 141 111 115 132 137 129 139 151 134
#> V V V V V V V V V V V V V V V V V V V V
#> 99 133 133 123 127 128 141 109 141 140 136 102 114 126 136 120 144 132 127 122
#> V V V V V V V V V V V V V V V V V V V V
#> 142 129 114 139 136 129 153 150 139 148 113 106 132 143 139 129 147 119 140 125
#> V V V V V V V V V V V V V V V V V V V V
#> 126 121 119 134 142 145 117 135 127 133 111 133 136 132 130 106 132 123 140 130
#> V V V V V V V V V V V V V V V V V V V V
#> 128 131 127 138 129 132 126 121 120 115 137 123 140 131 110 133 149 129 139 149
#>
#> $PPI_V
#> PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V
#> 198 178 179 191 173 172 210 192 219 192 178 194 159
#> PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V
#> 188 193 186 182 202 166 190 192 178 189 176 189 161
#> PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V
#> 178 199 186 172 178 171 196 199 195 207 190 188 163
#> PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V
#> 170 162 186 192 184 207 198 201 199 186 201 169 178
#> PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V
#> 192 180 175 192 192 178 183 184 179 195 177 185 187
#> PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V
#> 173 205 191 185 192 174 175 195 193 188 201 191 182
#> PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V
#> 190 209 193 199 183 186 194 181 191 199 187 201 197
#> PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V PPI_V
#> 201 182 200 180 169 204 200 198 185
#>
#> $bifan
#> bifan bifan bifan bifan bifan bifan bifan bifan bifan bifan bifan bifan bifan
#> 0 0 0 0 0 0 0 0 0 0 0 0 0
#> bifan bifan bifan bifan bifan bifan bifan bifan bifan bifan bifan bifan bifan
#> 0 0 0 0 0 0 0 0 0 1 0 0 0
#> bifan bifan bifan bifan bifan bifan bifan bifan bifan bifan bifan bifan bifan
#> 0 0 0 0 0 0 0 0 0 0 0 0 0
#> bifan bifan bifan bifan bifan bifan bifan bifan bifan bifan bifan bifan bifan
#> 0 0 0 0 0 0 0 0 0 0 0 0 0
#> bifan bifan bifan bifan bifan bifan bifan bifan bifan bifan bifan bifan bifan
#> 0 0 0 0 0 0 0 0 0 0 0 0 0
#> bifan bifan bifan bifan bifan bifan bifan bifan bifan bifan bifan bifan bifan
#> 0 0 0 0 0 0 0 0 0 0 0 0 0
#> bifan bifan bifan bifan bifan bifan bifan bifan bifan bifan bifan bifan bifan
#> 0 0 0 0 0 0 0 0 0 0 0 0 0
#> bifan bifan bifan bifan bifan bifan bifan bifan bifan
#> 0 0 0 0 0 0 0 0 0
# Create list of observed frequencies
observed <- list(
lambda = length(lambda),
bifan = length(bifan),
V = length(v),
PPI_V = length(ppi_v),
delta = length(delta)
)
calculate_Z(observed, nulls)
#> lambda delta V PPI_V bifan
#> 8.856408 -1.068636 -1.560671 113.300559 9.900000Now that you have Z-scores, you can use a cut-off of your choice to define significance.
Evaluting interaction similarity
Finally, another interesting pattern you may want to analyze is the interaction similarity between paralogous gene pairs. Previous studies have demonstrated that the Sorensen-Dice similarity is a suitable index for interaction similarity (Defoort, Van de Peer, and Carretero-Paulet 2019; Mottes et al. 2021), which is defined as:
\[ S(A,B) = \frac{2 \left| A \cap B \right|}{ \left|A \right| + \left| B \right|} \]
where A and B are the interacting partners of nodes A and B. To
calculate the Sorensen-Dice similarity for paralogous gene pairs, you
can use the function sd_similarity(). Let’s demonstrate it
by calculating the similarity between paralogs in the PPI network.
sim <- sd_similarity(gma_ppi, paralogs)
head(sim)
#> duplicate1 duplicate2 sorensen_dice
#> 11631 Glyma.01G004300 Glyma.05G223800 1
#> 11696 Glyma.01G205300 Glyma.05G064600 1
#> 11706 Glyma.01G207700 Glyma.05G061400 1
#> 12157 Glyma.01G004300 Glyma.08G030900 1
#> 12803 Glyma.01G207700 Glyma.11G034700 1
#> 13298 Glyma.01G163300 Glyma.16G123100 1
summary(sim$sorensen_dice)
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 0.2200 1.0000 1.0000 0.9812 1.0000 1.0000Session information
This document was created under the following conditions:
sessioninfo::session_info()
#> ─ Session info ───────────────────────────────────────────────────────────────
#> setting value
#> version R version 4.2.1 (2022-06-23)
#> os Ubuntu 20.04.4 LTS
#> system x86_64, linux-gnu
#> ui X11
#> language en
#> collate en_US.UTF-8
#> ctype en_US.UTF-8
#> tz UTC
#> date 2023-03-14
#> pandoc 2.18 @ /usr/local/bin/ (via rmarkdown)
#>
#> ─ Packages ───────────────────────────────────────────────────────────────────
#> package * version date (UTC) lib source
#> BiocManager 1.30.20 2023-02-24 [1] RSPM (R 4.2.0)
#> BiocParallel 1.30.4 2022-10-11 [1] Bioconductor
#> BiocStyle * 2.24.0 2022-04-26 [1] Bioconductor
#> bookdown 0.33 2023-03-06 [1] RSPM (R 4.2.0)
#> bslib 0.4.2 2022-12-16 [2] RSPM (R 4.2.0)
#> cachem 1.0.7 2023-02-24 [2] RSPM (R 4.2.0)
#> cli 3.6.0 2023-01-09 [2] RSPM (R 4.2.0)
#> codetools 0.2-19 2023-02-01 [3] RSPM (R 4.2.0)
#> desc 1.4.2 2022-09-08 [2] RSPM (R 4.2.0)
#> digest 0.6.31 2022-12-11 [2] RSPM (R 4.2.0)
#> evaluate 0.20 2023-01-17 [2] RSPM (R 4.2.0)
#> fastmap 1.1.1 2023-02-24 [2] RSPM (R 4.2.0)
#> fs 1.6.1 2023-02-06 [2] RSPM (R 4.2.0)
#> glue 1.6.2 2022-02-24 [2] CRAN (R 4.2.0)
#> highr 0.10 2022-12-22 [2] RSPM (R 4.2.0)
#> htmltools 0.5.4 2022-12-07 [2] RSPM (R 4.2.0)
#> jquerylib 0.1.4 2021-04-26 [2] CRAN (R 4.2.0)
#> jsonlite 1.8.4 2022-12-06 [2] RSPM (R 4.2.0)
#> knitr 1.42 2023-01-25 [2] RSPM (R 4.2.0)
#> lifecycle 1.0.3 2022-10-07 [2] RSPM (R 4.2.0)
#> magrene * 1.1.0 2023-03-14 [1] Bioconductor
#> magrittr 2.0.3 2022-03-30 [2] CRAN (R 4.2.0)
#> memoise 2.0.1 2021-11-26 [2] CRAN (R 4.2.0)
#> pkgdown 2.0.7 2022-12-14 [2] RSPM (R 4.2.0)
#> purrr 1.0.1 2023-01-10 [2] RSPM (R 4.2.0)
#> R6 2.5.1 2021-08-19 [2] CRAN (R 4.2.0)
#> ragg 1.2.5 2023-01-12 [2] RSPM (R 4.2.0)
#> rlang 1.0.6 2022-09-24 [2] RSPM (R 4.2.0)
#> rmarkdown 2.20 2023-01-19 [2] RSPM (R 4.2.0)
#> rprojroot 2.0.3 2022-04-02 [2] CRAN (R 4.2.0)
#> sass 0.4.5 2023-01-24 [2] RSPM (R 4.2.0)
#> sessioninfo 1.2.2 2021-12-06 [2] RSPM (R 4.2.0)
#> stringi 1.7.12 2023-01-11 [2] RSPM (R 4.2.0)
#> stringr 1.5.0 2022-12-02 [2] RSPM (R 4.2.0)
#> systemfonts 1.0.4 2022-02-11 [2] RSPM (R 4.2.0)
#> textshaping 0.3.6 2021-10-13 [2] RSPM (R 4.2.0)
#> vctrs 0.5.2 2023-01-23 [2] RSPM (R 4.2.0)
#> xfun 0.37 2023-01-31 [2] RSPM (R 4.2.0)
#> yaml 2.3.7 2023-01-23 [2] RSPM (R 4.2.0)
#>
#> [1] /__w/_temp/Library
#> [2] /usr/local/lib/R/site-library
#> [3] /usr/local/lib/R/library
#>
#> ──────────────────────────────────────────────────────────────────────────────